ESTATÍSTICA INFERENCIAL
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 492.)
Devido aos tempos e altos custos das mudanças de turno, um diretor de fabricação precisa convencer a administração de que um proposto método de fabricação reduz os custos antes que o novo método possa ser implementado. O método corrente de produção opera com um custo médio de US$ 220 por hora. Uma pesquisa está para ser realizada em que o custo do novo método será medido com relação a um período de produção de amostra.
Assinale a alternativa que indica as hipóteses nula e alternativa que são as mais apropriadas para este estudo.
H0: µ ≥ US$ 220 e Ha: µ < US$ 220.
H0: µ ≠ US$ 220 e Ha: µ = US$ 220.
H0: µ > US$ 220 e Ha: µ ≤ US$ 220.
H0: µ ≤ US$ 220 e Ha: µ > US$ 220.
H0: µ = US$ 220 e Ha: µ ≠ US$ 220.

A correlação entre o preço do produto e a quantidade vendida é positiva e r = 1.
A correlação entre o preço do produto e a quantidade vendida é negativa e – 1 < r < 0.
A correlação entre o preço do produto e a quantidade vendida é negativa e r = -1.
A correlação entre o preço do produto e a quantidade vendida é positiva e 0 < r < 1.
A correlação entre o preço do produto e a quantidade vendida é nula.
O gestor financeiro de uma rede de lojas de armarinhos estimou a equação
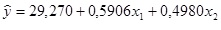
para prever o faturamento bruto mensal das lojas da rede, em que X1 = número de habitantes da zona urbana do município onde se localiza a loja (valores em 1.000) ; X2 = renda do município onde se localiza a loja (valores em milhões de R$).
Com base na equação estimada, julgue as seguintes afirmações:
- Há uma relação inversamente proporcional entre o faturamento bruto de uma loja e o número de habitantes da zona urbana de um município.
- Há uma relação diretamente proporcional entre o faturamento bruto de uma loja e a renda do município.
- Se o número de habitantes da zona urbana de determinado município for de 100 mil habitantes e a renda municipal for de R$ 320 milhões, o faturamento bruto previsto para a loja é de R$ 247,69 milhões.
Estão CORRETAS as afirmações:
2, apenas.
1 e 3, apenas.
3, apenas.
1 e 2, apenas.
2 e 3, apenas.
Em um levantamento, o valor planejado para a proporção p é 0,35. Que tamanho deve ter uma amostra para fornecer um intervalo de confiança de 95% com uma margem de erro de 0,05? Faça os cálculos com seis casas decimais e arredonde o resultado final para um número inteiro.
Dados adicionais:

Z = 1,96.
250 elementos.
401 elementos.
520 elementos.
295 elementos.
350 elementos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 492.)
O proprietário da Showtime Movie Theaters, Inc., gostaria de estimar o faturamento bruto semanal como função dos gastos com publicidade. Dados históricos para uma amostra de seis semanas são apresentados a seguir.

Considerando ambos os anúncios, de televisão e de jornal, como variáveis independentes, os dados foram inseridos em uma planilha eletrônica Excel, a qual gerou o seguinte relatório de saída:

Com base no relatório de saída do Excel, julgue as seguintes afirmações a respeito da equação estimada:
I. O anúncio de televisão e o anúncio de jornal, em conjunto, explicam 91,9% das variações no faturamento bruto semanal da Showtime Movie Theaters, Inc.
II. A equação de regressão estimada é igual a 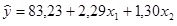
III. Há uma relação estatística significante entre o faturamento bruto semanal da empresa, o anúncio de televisão e o anúncio de jornal, pois a análise da variância mostra que o F teste = 28,38 é maior que o F crítico = 5,79, com 5% de significância.
IV. A equação de regressão estimada permite afirmar que quanto menos a empresa anunciar na televisão e no jornal maior o seu faturamento bruto semanal.
Estão corretas as afirmações:
I, II e III, somente.
I e II, somente.
I, II, III e IV.
I, II e IV, somente.
II, III e IV, somente.
Ao se dispor os dados sobre preço e quantidade vendida de determinado produto em um diagrama de dispersão, obteve-se o seguinte gráfico:
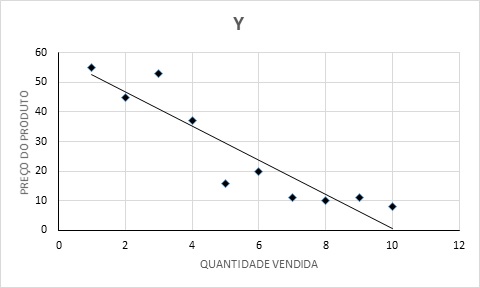
Chamando Y: preço do produto; X: quantidade vendida do produto; rxy = correlação entre X e Y, com base no diagrama de dispersão, é correto afirmar que:
A correlação entre X e Y é negativa e – 1 < r < 0.
A correlação entre X e Y é negativa e r = -1.
A correlação entre X e Y é nula.
A correlação entre X e Y é positiva e r = 1.
A correlação entre X e Y é positiva e 0 < r < 1.

A porcentagem de mulheres empregadas nas companhias é diretamente proporcional à porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias aumenta a porcentagem de mulheres que ocupam cargos de gerência.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias diminui a porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.

c
a
d
b
e

A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
H0: µ ≥ US$ 220 e Ha: µ < US$ 220.
H0: µ ≠ US$ 220 e Ha: µ = US$ 220.
H0: µ > US$ 220 e Ha: µ ≤ US$ 220.
H0: µ ≤ US$ 220 e Ha: µ > US$ 220.
H0: µ = US$ 220 e Ha: µ ≠ US$ 220.

A correlação entre o preço do produto e a quantidade vendida é positiva e r = 1.
A correlação entre o preço do produto e a quantidade vendida é negativa e – 1 < r < 0.
A correlação entre o preço do produto e a quantidade vendida é negativa e r = -1.
A correlação entre o preço do produto e a quantidade vendida é positiva e 0 < r < 1.
A correlação entre o preço do produto e a quantidade vendida é nula.
O gestor financeiro de uma rede de lojas de armarinhos estimou a equação
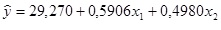
para prever o faturamento bruto mensal das lojas da rede, em que X1 = número de habitantes da zona urbana do município onde se localiza a loja (valores em 1.000) ; X2 = renda do município onde se localiza a loja (valores em milhões de R$).
Com base na equação estimada, julgue as seguintes afirmações:
- Há uma relação inversamente proporcional entre o faturamento bruto de uma loja e o número de habitantes da zona urbana de um município.
- Há uma relação diretamente proporcional entre o faturamento bruto de uma loja e a renda do município.
- Se o número de habitantes da zona urbana de determinado município for de 100 mil habitantes e a renda municipal for de R$ 320 milhões, o faturamento bruto previsto para a loja é de R$ 247,69 milhões.
Estão CORRETAS as afirmações:
2, apenas.
1 e 3, apenas.
3, apenas.
1 e 2, apenas.
2 e 3, apenas.
Em um levantamento, o valor planejado para a proporção p é 0,35. Que tamanho deve ter uma amostra para fornecer um intervalo de confiança de 95% com uma margem de erro de 0,05? Faça os cálculos com seis casas decimais e arredonde o resultado final para um número inteiro.
Dados adicionais:

Z = 1,96.
250 elementos.
401 elementos.
520 elementos.
295 elementos.
350 elementos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 492.)
O proprietário da Showtime Movie Theaters, Inc., gostaria de estimar o faturamento bruto semanal como função dos gastos com publicidade. Dados históricos para uma amostra de seis semanas são apresentados a seguir.

Considerando ambos os anúncios, de televisão e de jornal, como variáveis independentes, os dados foram inseridos em uma planilha eletrônica Excel, a qual gerou o seguinte relatório de saída:

Com base no relatório de saída do Excel, julgue as seguintes afirmações a respeito da equação estimada:
I. O anúncio de televisão e o anúncio de jornal, em conjunto, explicam 91,9% das variações no faturamento bruto semanal da Showtime Movie Theaters, Inc.
II. A equação de regressão estimada é igual a 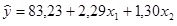
III. Há uma relação estatística significante entre o faturamento bruto semanal da empresa, o anúncio de televisão e o anúncio de jornal, pois a análise da variância mostra que o F teste = 28,38 é maior que o F crítico = 5,79, com 5% de significância.
IV. A equação de regressão estimada permite afirmar que quanto menos a empresa anunciar na televisão e no jornal maior o seu faturamento bruto semanal.
Estão corretas as afirmações:
I, II e III, somente.
I e II, somente.
I, II, III e IV.
I, II e IV, somente.
II, III e IV, somente.
Ao se dispor os dados sobre preço e quantidade vendida de determinado produto em um diagrama de dispersão, obteve-se o seguinte gráfico:

Chamando Y: preço do produto; X: quantidade vendida do produto; rxy = correlação entre X e Y, com base no diagrama de dispersão, é correto afirmar que:
A correlação entre X e Y é negativa e – 1 < r < 0.
A correlação entre X e Y é negativa e r = -1.
A correlação entre X e Y é nula.
A correlação entre X e Y é positiva e r = 1.
A correlação entre X e Y é positiva e 0 < r < 1.

A porcentagem de mulheres empregadas nas companhias é diretamente proporcional à porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias aumenta a porcentagem de mulheres que ocupam cargos de gerência.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias diminui a porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.

c
a
d
b
e

A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
A correlação entre o preço do produto e a quantidade vendida é positiva e r = 1.
A correlação entre o preço do produto e a quantidade vendida é negativa e – 1 < r < 0.
A correlação entre o preço do produto e a quantidade vendida é negativa e r = -1.
A correlação entre o preço do produto e a quantidade vendida é positiva e 0 < r < 1.
A correlação entre o preço do produto e a quantidade vendida é nula.
O gestor financeiro de uma rede de lojas de armarinhos estimou a equação
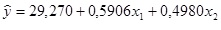
para prever o faturamento bruto mensal das lojas da rede, em que X1 = número de habitantes da zona urbana do município onde se localiza a loja (valores em 1.000) ; X2 = renda do município onde se localiza a loja (valores em milhões de R$).
Com base na equação estimada, julgue as seguintes afirmações:
- Há uma relação inversamente proporcional entre o faturamento bruto de uma loja e o número de habitantes da zona urbana de um município.
- Há uma relação diretamente proporcional entre o faturamento bruto de uma loja e a renda do município.
- Se o número de habitantes da zona urbana de determinado município for de 100 mil habitantes e a renda municipal for de R$ 320 milhões, o faturamento bruto previsto para a loja é de R$ 247,69 milhões.
Estão CORRETAS as afirmações:
2, apenas.
1 e 3, apenas.
3, apenas.
1 e 2, apenas.
2 e 3, apenas.
Em um levantamento, o valor planejado para a proporção p é 0,35. Que tamanho deve ter uma amostra para fornecer um intervalo de confiança de 95% com uma margem de erro de 0,05? Faça os cálculos com seis casas decimais e arredonde o resultado final para um número inteiro.
Dados adicionais:

Z = 1,96.
250 elementos.
401 elementos.
520 elementos.
295 elementos.
350 elementos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 492.)
O proprietário da Showtime Movie Theaters, Inc., gostaria de estimar o faturamento bruto semanal como função dos gastos com publicidade. Dados históricos para uma amostra de seis semanas são apresentados a seguir.

Considerando ambos os anúncios, de televisão e de jornal, como variáveis independentes, os dados foram inseridos em uma planilha eletrônica Excel, a qual gerou o seguinte relatório de saída:

Com base no relatório de saída do Excel, julgue as seguintes afirmações a respeito da equação estimada:
I. O anúncio de televisão e o anúncio de jornal, em conjunto, explicam 91,9% das variações no faturamento bruto semanal da Showtime Movie Theaters, Inc.
II. A equação de regressão estimada é igual a 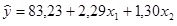
III. Há uma relação estatística significante entre o faturamento bruto semanal da empresa, o anúncio de televisão e o anúncio de jornal, pois a análise da variância mostra que o F teste = 28,38 é maior que o F crítico = 5,79, com 5% de significância.
IV. A equação de regressão estimada permite afirmar que quanto menos a empresa anunciar na televisão e no jornal maior o seu faturamento bruto semanal.
Estão corretas as afirmações:
I, II e III, somente.
I e II, somente.
I, II, III e IV.
I, II e IV, somente.
II, III e IV, somente.
Ao se dispor os dados sobre preço e quantidade vendida de determinado produto em um diagrama de dispersão, obteve-se o seguinte gráfico:

Chamando Y: preço do produto; X: quantidade vendida do produto; rxy = correlação entre X e Y, com base no diagrama de dispersão, é correto afirmar que:
A correlação entre X e Y é negativa e – 1 < r < 0.
A correlação entre X e Y é negativa e r = -1.
A correlação entre X e Y é nula.
A correlação entre X e Y é positiva e r = 1.
A correlação entre X e Y é positiva e 0 < r < 1.

A porcentagem de mulheres empregadas nas companhias é diretamente proporcional à porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias aumenta a porcentagem de mulheres que ocupam cargos de gerência.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias diminui a porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.

c
a
d
b
e

A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
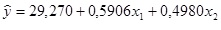
2, apenas.
1 e 3, apenas.
3, apenas.
1 e 2, apenas.
2 e 3, apenas.
Em um levantamento, o valor planejado para a proporção p é 0,35. Que tamanho deve ter uma amostra para fornecer um intervalo de confiança de 95% com uma margem de erro de 0,05? Faça os cálculos com seis casas decimais e arredonde o resultado final para um número inteiro.
Dados adicionais:

Z = 1,96.
250 elementos.
401 elementos.
520 elementos.
295 elementos.
350 elementos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 492.)
O proprietário da Showtime Movie Theaters, Inc., gostaria de estimar o faturamento bruto semanal como função dos gastos com publicidade. Dados históricos para uma amostra de seis semanas são apresentados a seguir.

Considerando ambos os anúncios, de televisão e de jornal, como variáveis independentes, os dados foram inseridos em uma planilha eletrônica Excel, a qual gerou o seguinte relatório de saída:

Com base no relatório de saída do Excel, julgue as seguintes afirmações a respeito da equação estimada:
I. O anúncio de televisão e o anúncio de jornal, em conjunto, explicam 91,9% das variações no faturamento bruto semanal da Showtime Movie Theaters, Inc.
II. A equação de regressão estimada é igual a 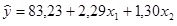
III. Há uma relação estatística significante entre o faturamento bruto semanal da empresa, o anúncio de televisão e o anúncio de jornal, pois a análise da variância mostra que o F teste = 28,38 é maior que o F crítico = 5,79, com 5% de significância.
IV. A equação de regressão estimada permite afirmar que quanto menos a empresa anunciar na televisão e no jornal maior o seu faturamento bruto semanal.
Estão corretas as afirmações:
I, II e III, somente.
I e II, somente.
I, II, III e IV.
I, II e IV, somente.
II, III e IV, somente.
Ao se dispor os dados sobre preço e quantidade vendida de determinado produto em um diagrama de dispersão, obteve-se o seguinte gráfico:

Chamando Y: preço do produto; X: quantidade vendida do produto; rxy = correlação entre X e Y, com base no diagrama de dispersão, é correto afirmar que:
A correlação entre X e Y é negativa e – 1 < r < 0.
A correlação entre X e Y é negativa e r = -1.
A correlação entre X e Y é nula.
A correlação entre X e Y é positiva e r = 1.
A correlação entre X e Y é positiva e 0 < r < 1.

A porcentagem de mulheres empregadas nas companhias é diretamente proporcional à porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias aumenta a porcentagem de mulheres que ocupam cargos de gerência.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias diminui a porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.

c
a
d
b
e

A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
250 elementos.
401 elementos.
520 elementos.
295 elementos.
350 elementos.
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 492.)
O proprietário da Showtime Movie Theaters, Inc., gostaria de estimar o faturamento bruto semanal como função dos gastos com publicidade. Dados históricos para uma amostra de seis semanas são apresentados a seguir.

Considerando ambos os anúncios, de televisão e de jornal, como variáveis independentes, os dados foram inseridos em uma planilha eletrônica Excel, a qual gerou o seguinte relatório de saída:

Com base no relatório de saída do Excel, julgue as seguintes afirmações a respeito da equação estimada:
I. O anúncio de televisão e o anúncio de jornal, em conjunto, explicam 91,9% das variações no faturamento bruto semanal da Showtime Movie Theaters, Inc.
II. A equação de regressão estimada é igual a 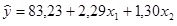
III. Há uma relação estatística significante entre o faturamento bruto semanal da empresa, o anúncio de televisão e o anúncio de jornal, pois a análise da variância mostra que o F teste = 28,38 é maior que o F crítico = 5,79, com 5% de significância.
IV. A equação de regressão estimada permite afirmar que quanto menos a empresa anunciar na televisão e no jornal maior o seu faturamento bruto semanal.
Estão corretas as afirmações:
I, II e III, somente.
I e II, somente.
I, II, III e IV.
I, II e IV, somente.
II, III e IV, somente.
Ao se dispor os dados sobre preço e quantidade vendida de determinado produto em um diagrama de dispersão, obteve-se o seguinte gráfico:

Chamando Y: preço do produto; X: quantidade vendida do produto; rxy = correlação entre X e Y, com base no diagrama de dispersão, é correto afirmar que:
A correlação entre X e Y é negativa e – 1 < r < 0.
A correlação entre X e Y é negativa e r = -1.
A correlação entre X e Y é nula.
A correlação entre X e Y é positiva e r = 1.
A correlação entre X e Y é positiva e 0 < r < 1.

A porcentagem de mulheres empregadas nas companhias é diretamente proporcional à porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias aumenta a porcentagem de mulheres que ocupam cargos de gerência.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias diminui a porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.

c
a
d
b
e

A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
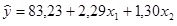
I, II e III, somente.
I e II, somente.
I, II, III e IV.
I, II e IV, somente.
II, III e IV, somente.
Ao se dispor os dados sobre preço e quantidade vendida de determinado produto em um diagrama de dispersão, obteve-se o seguinte gráfico:

Chamando Y: preço do produto; X: quantidade vendida do produto; rxy = correlação entre X e Y, com base no diagrama de dispersão, é correto afirmar que:
A correlação entre X e Y é negativa e – 1 < r < 0.
A correlação entre X e Y é negativa e r = -1.
A correlação entre X e Y é nula.
A correlação entre X e Y é positiva e r = 1.
A correlação entre X e Y é positiva e 0 < r < 1.

A porcentagem de mulheres empregadas nas companhias é diretamente proporcional à porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias aumenta a porcentagem de mulheres que ocupam cargos de gerência.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias diminui a porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.

c
a
d
b
e

A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:

A correlação entre X e Y é negativa e – 1 < r < 0.
A correlação entre X e Y é negativa e r = -1.
A correlação entre X e Y é nula.
A correlação entre X e Y é positiva e r = 1.
A correlação entre X e Y é positiva e 0 < r < 1.

A porcentagem de mulheres empregadas nas companhias é diretamente proporcional à porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias aumenta a porcentagem de mulheres que ocupam cargos de gerência.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias diminui a porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.

c
a
d
b
e

A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
A porcentagem de mulheres empregadas nas companhias é diretamente proporcional à porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias aumenta a porcentagem de mulheres que ocupam cargos de gerência.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias diminui a porcentagem de mulheres que ocupam cargos de gerência.
À medida que diminui a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.
À medida que aumenta a porcentagem de mulheres empregadas nas companhias a porcentagem de mulheres que ocupam cargos de gerência permanece à mesma.

c
a
d
b
e

A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
c
a
d
b
e

A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
A média dos pesos das peças é 23,25 Kg.
A média dos preços das peças em unidades monetárias é 350,15
O valor do estimador A é igual a 8,05
O valor do estimador B é igual a 120,78
A equação de regressão linear é dada por Y = 9,49 x + 125,79
(Adaptada de ANDERSON, David R.; SWEENEY, Dennis J.; WILLIAMS, Thomas A. Estatística aplicada à administração e economia. São Paulo: Pioneira Thomson Learning, 2002, p. 499.)
Em um processo de manufatura a velocidade da linha de montagem (metros por minuto) foi culpada de afetar o número de partes defeituosas em um processo de inspeção. Para testar essa teoria, os gerentes idealizaram uma situação na qual o mesmo lote de partes foi inspecionado visualmente em uma variedade de velocidades da linha de montagem. A tabela seguinte lista os dados coletados.

Os resultados de saída da planilha eletrônica Excel apresentam os seguintes resultados.

Com base nos dados do relatório de saída do Excel, julgue as seguintes afirmações:
1. A velocidade da linha é a variável explicativa e o número de partes defeituosas encontradas é a variável explicada no modelo.
2. A equação de regressão estimada é 
3. Como t calculado = -3,3665 é menor que t crítico = - 1,533, conclui-se que a velocidade da linha não influi no número de partes defeituosas encontradas no processo de inspeção.
4. De acordo com a equação estimada, quanto menor a velocidade da linha maior o número de partes defeituosas encontradas no processo de inspeção.
Estão corretas as afirmações:
